몬티홀 문제를 아시고, 풀이도 이해하고 계신분은 마지막 1, 2 숫자 문단으로 바로 넘어가시면 되겠습니다.

몬티홀 문제를 먼저 소개합니다.

미국의 TV게임쇼에서 유래된 딜레마문제인데, 여러분은 게임 참가자입니다. 세개의 닫힌 문이있고, 그 문중 두개의 문 뒤에는 염소가 있고, 나머지 하나의 문 뒤에는 고급 자동차가 있습니다.

여러분이 한번의 기회로, 고급 자동차가 있는 문을 선택한다면, 그 자동차를 상품으로 획득할 수 있습니다.

여러분은 세개의 문중 하나를 골랐습니다. 그런데 사회자가 이때 제안합니다. "제가 당신이 고르지 않은 두개의 문 중, 염소가 있는 하나의 문을 열어서 보여드리겠습니다!" 그리고는 진짜로 문을 열어 염소가 있는 다른 문을 확인시켜주었습니다.

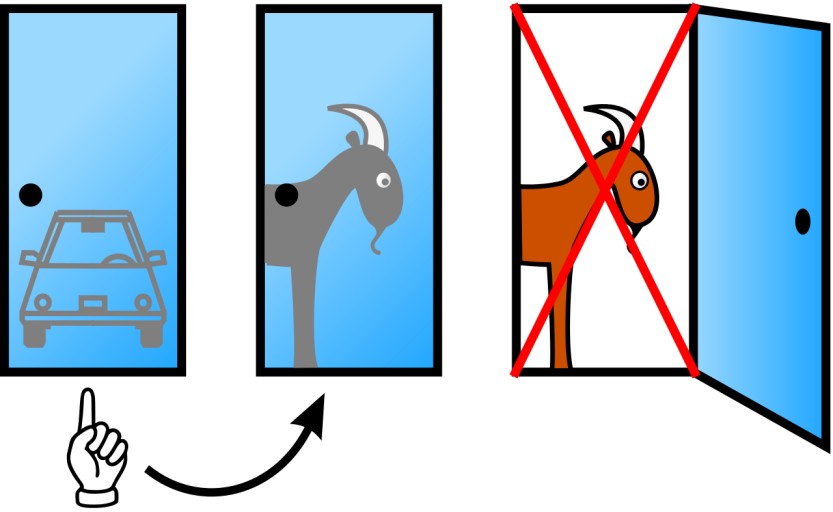
그리고는 사회자가 말합니다. "선택을 바꾸실 기회를 한번 드리겠습니다. 선택을 바꾸시겠습니까"

여기서 문제입니다. 선택을 바꾸는 것이 나을까요?

이 문제의 답은 선택을 바꾸는 것이 낫다 입니다.

언뜻 보기엔 남은 문이 두개고 하나는 자동차, 하나는 염소이므로 확률이 반반이라 생각할 수 있지만,

처음에 골랐던 문이 염소일 확률이 2/3이므로, 나머지 하나가 공개되었을 때, 선택을 바꿔서 자동차일 확률이 그대로 2/3인 것입니다.

이 문제를 보다가 궁금한 점이 두가지 생겼습니다.

1. 조건을 조금 바꿔보겠습니다. 전지전능한 사회자가 없는 상황이고, 당신과 제가 서로 대결하는 게임을 하고 있는 상황입니다.

서로 번갈아서 문을 열어 먼저 자동차를 찾는 사람이 이기는 게임입니다. 그리고, 제가 선턴입니다.

당신은 마음속으로 문을 하나 골라놓았습니다.

웬걸 제가 당신이 고른 문이 아닌 다른 문을 골랐고, 그 뒤엔 다행히 염소가 있었습니다.

이 때도 당신은 선택을 바꾸는 것이 나을까요?

앞선 문제와의 차이점은 사회자가 염소가 있는 문을 알고 열어준 것이 아니라, 악당인 저 또한 아무것도 모르는 상황에서 확률적으로 당신이 선택하지 않은, 염소를 골랐다는 것입니다.

제 생각에 답은 똑같이 바꾸는게 2/3확률로 낫다 일 것 같긴 한데 확신이 안들어요ㅠㅠ

2. 처음 상황과 똑같습니다. 하지만 이번엔 문이 네개입니다. (차 1 염소 3)

여러분은 하나의 문을 골랐고, 사회자가 남은 세개의 문중 염소가 있는 문을 하나 열어서 보여주어서 이제 남은 문이 세개가 되었습니다.

이때도 선택을 바꾸는 것이 맞을까요?

제 생각은 처음에 고른 것이 염소일 확률이 3/4이고, 이때 남은 문들 중 선택을 바꿔서 자동차일 확률이 1/2이므로, 전체적으로는 선택을 바꿔서 자동차일 확률이 (3/4)X(1/2)=3/8 이므로 바꾸지 않는 것이 낫다......?라는 생각을 했는데 바꾸지 않고 맞을 확률이 5/8나 된다고? 뭔가 이상해요.

제 계산방식의 오류를 찾아주시면 감사하겠습니다.

(글을 쓰던 도중 2번 궁금증은 혼자서 해결이 된 것 같습니다. 다만 재밌으니까 지우지 않고 여러분께도 맡겨보겠습니다!)