미궁게임 더라비린스
  • 미궁게임
  • 게시판
[2020-08-23] 기하 문제 P human 00:35:08 P100 클리어 32명 참여 47명
 



그리기 모드 추가 기념 기하 문제입니다.


AB=CD, ∠ACB=30°,  ∠BAD=45° 인 등변사다리꼴 ABCD가 있다.


점 A, B, C, D를 지나고 중심이 O인 원을 그리고 점 C, B, A를 직선 DO에 대해 대칭 한 점을 각각 E라 하자.


△DFA가 △CEG보다 어둡다고 할 때, △BDF의 이름을 알파벳 4글자로 쓰시오.

정답과 해설 보기

bdim


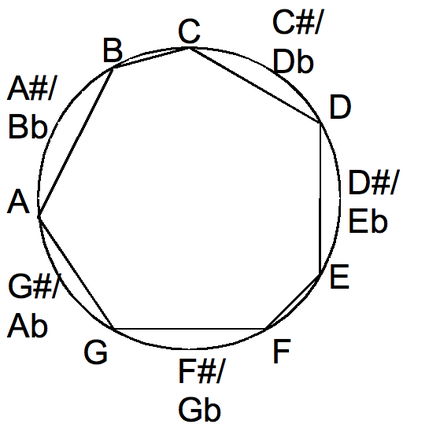
작도된 점들은 반음계(https://en.wikipedia.org/wiki/Chromatic_circle)의 관계를 보입니다. 


그러므로 삼각형은 3개의 음, 즉, 화음을 나타낸다는 것을 알 수 있습니다.


밝다 어둡다는 각각 장조, 단조를 나타내는 힌트이고요.


따라서 정답은 B, D, F의 화음인 Diminished B, 즉 , Bdim이 됩니다.


댓글

10분마다 갱신됩니다.